barabasi graph - Returns a random graph using Barabási–Albert preferential attachment. A graph of n nodes is grown by attaching new nodes each with m edges that are preferentially attached to existing nodes with high degree.
barbell graph - Returns the Barbell Graph: two complete graphs connected by a path. This graph is an extremal example in David Aldous and Jim Fill’s e-text on Random Walks on Graphs.
bipartite graph - Returns the complete bipartite graph K_{n_1,n_2}. The graph is composed of two partitions with nodes 0 to (n1 - 1) in the first and nodes n1 to (n1 + n2 - 1) in the second. Each node in the first is connected to each node in the second.
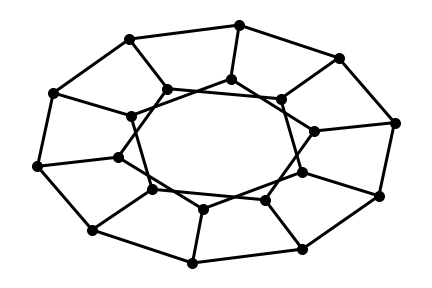
dodecahedral graph - The dodecahedral graph is the Platonic graph corresponding to the connectivity of the vertices of a dodecahedron, illustrated is one of many examples below.
import networkx as nx
G = nx.Graph()
G = nx.dodecahedral_graph()
options = {
'node_color': 'black',
'node_size': 100,
'width': 3,
}
shells = [[2, 3, 4, 5, 6], [8, 1, 0, 19, 18, 17, 16, 15, 14, 7], [9, 10, 11, 12, 13]]
nx.draw_shell(G, nlist=shells, **options)
nx.draw(G, **options)
plt.savefig("path.png")
erdos renyi graph - Returns a random graph, also known as an Erdős-Rényi graph or a binomial graph.
lollipop graph - This is the Barbell Graph without the right barbell.
petersen graph - The Peterson graph is a cubic, undirected graph with 10 nodes and 15 edges. Julius Petersen constructed the graph as the smallest counterexample against the claim that a connected bridgeless cubic graph has an edge colouring with three colours.
random lobster graph - A lobster is a tree that reduces to a caterpillar when pruning all leaf nodes. A caterpillar is a tree that reduces to a path graph when pruning all leaf nodes; setting p2 to zero produces a caterpillar. This implementation iterates on the probabilities p1 and p2 to add edges at levels 1 and 2, respectively. Graphs are therefore constructed iteratively with uniform randomness at each level rather than being selected uniformly at random from the set of all possible lobsters.
tetrahedral graph - The tetrahedral graph has a single minimal integral embedding, illustrated above (Harborth and Möller 1994), with maximum edge length 4.
Tetrahedral graph has 4 nodes and 6 edges. It is a special case of the complete graph, K4, and wheel graph, W4. It is one of the 5 platonic graphs.
tutte graph - The Tutte graph is a cubic polyhedral, non-Hamiltonian graph. It has 46 nodes and 69 edges. It is a counterexample to Tait’s conjecture that every 3-regular polyhedron has a Hamiltonian cycle. It can be realized geometrically from a tetrahedron by multiply truncating three of its vertices.
watts strogatz graph - small-world graph.
コメント